Power Transmission Lines as Capacitors

Last week, my mentor mentioned that high-voltage power transmission circuits could sometimes be used to provide reactive power support when on potential but off load, particularly for parallel lines.  Anecdotally, based on my limited understanding of the Ferranti Effect, this seems perfectly reasonable: light loading on the line results in elevated line charging capacitance, which is then injected to the system at the point of connection.

Ferranti Effect

In order to understand the results, we have to understand the cause behind the Ferranti Effect.

All transmission lines (even the kind discussed in Radiation and Propagation courses) behave the same way once the line length approaches a tenth of the signal wavelength.  Due to the relatively low frequency of utility power (60Hz in North America and 50Hz in many other parts of the world), the wavelength is pretty long, so these effects only begin to appear in significantly long (greater than 300km) transmission lines.

The classical model is:

Source: Wikipedia

Lines of a moderate length (greater than 300km) can be modelled simply as a series resistance, series inductance and shunt capacitance – in Power Systems, we often call this model a “Pi section” (this moniker makes more sense if you separate the capacitance at the sending and receiving ends of the line, dividing them by two).  Longer lines (those exceeding 500km) are then an extension of an already-solved problem: they can simply be modelled using multiple moderate-length segments as appropriate.

Keen readers will notice that this is, quite simply, a two-port network model: we can consider each Pi section a black box, with sending-end voltage/current and receiving-end voltage/current.  Many of us rely on an approximation of how wires behave: in most applications, they have infinitesimal impedance, and so the impedance may be neglected in calculations.  However, when we approach power transmission, the voltages and currents are much higher than experienced elsewhere, which can have quite a profound impact on system operation.

I hope that this brief discussion provided a reasonable introduction or review.  If not, the Kathmandu University also has a very good handout on the subject.

Surge Impedance Loading

Based on the telegrapher’s equations and the above model, we can determine the characteristic impedance (also called surge impedance) of the transmission line as:

In all transmission lines, for power or signals alike, optimal power transfer occurs when the load impedance matches the characteristic impedance.  In Power Systems, we like to relate these quantities to units Power (Real, Reactive and Apparent) because these quantities can always be directly compared regardless of phase angles, power factors, harmonic distortion levels or voltage levels.

The Surge Impedance Loading converts the characteristic impedance (ohms) into a power (Watts) value:

If the amount of power being transmitted equals the SIL, the line mutual coupling (the inductance and capacitance in the model) cancels each other out, thus resulting in the line operating at unity power factor.  When the amount of power transferred is below the SIL, the power factor is leading (capacitive), and when the amount of power transferred is above the SIL, the power factor is lagging (inductive).

An intuitive model

Intuitively, I understand this behaviour by thinking about the cause of these impedances, though I am not a physicist, so this intuition is best understood as a useful analogy, not as fact.  I imagine lines have some slight twist when installed, giving rise to the series inductance.  Likewise, lines are conductors of different potential separated by a dielectric (air), which results in some capacitive coupling between lines.

Recall that power loss due to the resistance of a power line can be calculated using Joule’s law:

Similarly, the reactive power absorbed by (or injected from, if Q is negative) a power line into the system can be calculated using (where X is defined as negative for capacitors and positive for inductors):

The inductance is fixed, but the amount of reactive power absorbed by the series inductance is proportional to the current flowing across the line.  On a lightly loaded line, or where the receiving end is an open circuit, the current is very small, so the inductive nature of the line is minimized and the capacitive behaviour dominates.  Thus, the line is below the SIL and operates with a leading (capacitive) power factor.

Power transmission lines as capacitors

Finally, to get to the real point of this article. Given the above background, it follows that lightly loaded or open-ended lines will inject reactive power. With lightly loaded parallel redundant lines, it is therefore possible to open one line and use it to provide reactive power (var) support for the system.

For my simulation, I used two parallel 230kV lines, each 600km long, with three ideally-transposed phases on each right-of-way (in delta configuration with four bundled sub-conductors). These lines were supplied by an infinite bus (voltage source at 22kVrms line-to-line) with a 22/230kV Wye-Delta transformer. At the receiving end, a 300MW+5Mvar load was installed.

Here are the two circuits in steady state (note that BRK2 is open):

 

Note that TLine1 has a depressed receiving end voltage due to the current flowing a cross that line (the line inductance cancels out the Ferranti effect), but TLine2 has an elevated receiving end voltage due to the Ferranti Effect. Also note that the reactive power flow at the sending end for TLine2 is negative, indicating that reactive power is flowing “backwards” to the sending end.

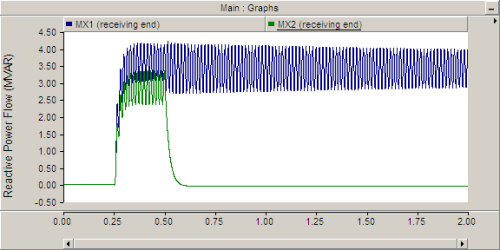
Let’s take a closer look at what’s happening at the receiving end:

 

The breakers were configured to begin open and close in at 250ms to energize the circuit. Afterward, BRK1 remained closed and BRK2 was reopened at 500ms. We can see that reactive power initially flows across both lines, but when the receiving end circuit breaker is opened, reactive power ceases to flow. Note that the x-axis shows elapsed time of the simulation (in seconds).

The sending end, by contrast, is much more interesting:

 

When both breakers are opened (until 250ms), there is a significant line charging capacitance drawing reactive power from the system. After the breakers close, the reactive power demand drops significantly (though it is still slightly capacitive due to both lines being lightly loaded). Once TLine2 is opened at the receiving end at 500ms, something interesting happens: the reactive power injected by that line into the system returns to its line-end-open state, while TLine1 increases its reactive power consumption in unison.

In conclusion, it is entirely possible to use a transmission line as a shunt capacitor.

What is x_authority?

The CPAN ecosystem is one of the most compelling reasons for the continued growth of the Perl programming language. It has been discussed at length by numerous people, and there have been several attempts to imitate this aspect of the Perl community through projects like: CRAN, CCAN, JSAN and more.

Unfortunately, in equal parts due to its age and design philosophy, the PAUSE system powering CPAN makes it difficult for distributions to be maintained by a group, rather than an individual. The inspiration for this post comes from a discussion I had recently with Florian Ragwitz, who contributes to several key Perl projects, including Catalyst, Moose, DBIx::Class and many more.

Permissions

First, a bit about how permissions on CPAN work.

In order to make a package installable using the CPAN Shell, there must be some mechanism to disambiguate a module name. Consider this simple example:

1. I upload Acme::Package to CPAN.
2. Some time passes, and unbeknownst to me, another author uploads a different package, but which is called Acme::Package to CPAN as well.

In the absence of any permission checking, if I then instructed users to install Acme::Package using the CPAN Shell, they would inadvertently install the wrong distribution! This has some rather serious implications: the other Acme::Package is probably quite different from mine, and a malicious author could have taken my software and added a backdoor vulnerability.

CPAN solves this issue by tracking each module namespace separately using the PAUSE Indexer, which assigns upload permissions to users through two mechanisms:

1. The module namespace registration list.
2. First-come status (the first uploader of a given package namespace “owns” that namespace).

Going back to the example given, the second uploader of Acme::Package would not have permission to use the namespace. The package will be accepted into the archive, but will not be indexed, meaning that users installing Acme::Package will still get my distribution.

If users want to install the other author’s package (which is marked as an UNAUTHORIZED upload in big red letters on CPAN Search), they would need to explicitly specify AUTHOR/Acme-Package-1.00.tar.gz.

For packages maintained by several people, it is also possible to assign co-maintainer status to others, so that they may also upload a package and have it correctly indexed. This way, two or more people can work on the same package together, and upload it under their own accounts (without causing the upload to be marked unauthorized). Thus, PAUSE credentials do not need to be shared.

This provides a nice solution to the malicious upload problem, but also has implications for team-maintained packages. In particular, consider the case where there are two authors working on Acme::Library.

1. Alice uploads the first version to CPAN, containing modules: Acme::Library and Acme::Library::Main.
2. The PAUSE Indexer grants Alice first-come permissions to both Acme::Library and Acme::Library::Main.
3. Alice grants Bob co-maintainer status on both Acme::Library and Acme::Library::Main.
4. Bob creates a new Acme::Library::Other module and adds it to the  package.
5. The PAUSE Indexer grants Bob first-come permissions to Acme::Library::Other.
6. Subsequent uploads by Alice will cause the upload of Acme::Library::Other to be marked UNAUTHORIZED.

Solutions

Clever Perl authors have attempted to solve this problem in many different ways over the years, but none of them have been widely successful because they all rely on some degree of human interaction.

Shared PAUSE Accounts

Some notable projects have attempted to solve the issue by creating a shared PAUSE user to hold the requisite first-come or module list upload permissions, which may then be granted to all other team members through the existing co-maintainer facility.

Alternatively, since it is easier for smaller projects, many modules simply assign first-come permissions to a single person, who is then in charge of providing co-maintainer permissions to others who would like to work on it.

Both of these approaches have the same limitation: any people uploading new modules must remember to assign first-come permissions to the group or user in question. In our case, Bob should have assigned first-come permissions to Acme::Library::Other to Alice, who then must pass co-maintainer permissions back to Bob. Unfortunately, this almost never happens, and Alice must chase down Bob (who happens to be on vacation in Antarctica) or, alternatively, the already over-worked PAUSE administrators.

Single Uploader

Some projects deal with this issue by sharing a version control system and having all the uploads go through a single person, in our case, Alice. This fixes the permission problem, since first-come permissions are always granted to Alice, but it results in a single point of failure. If there are some serious security issues requiring an immediate release, Alice must be available (and, as luck would have it, she is vacationing in Antarctica at the time).

Enter x_authority

One proposed solution, which is used in projects including Moose and Catalyst, is to use a special field in the CPAN Metadata file (META.yml or META.json) that defines someone as the “authority” for first-come namespaces in a distribution.

This is how it would work for Alice‘s Acme::Library distribution:

1. Alice uploads a package to CPAN, containing modules: Acme::Library and Acme::Library::Main.
2. Alice specifies, in META.yml:

   x_authority: cpan:ALICE

   This refers to Alice‘s PAUSE login, and is the person to whom permissions for new modules uploaded in this distribution are assigned.

3. Alice grants Bob co-maintainer status on both Acme::Library and Acme::Library::Main.
4. Bob creates a new Acme::Library::Other module and adds it to the package
5. The PAUSE indexer, seeing the x_authority defined in META.yml, grants Alice (not Bob!) first-come permissions to Acme::Library::Other. At this time, Bob also automatically gets co-maintainer permissions to Acme::Library::Other.
6. Subsequent uploads by Alice will be indexed properly.

Problems

There are still some outstanding issues that need to be resolved, but the x_authority proposal represents a giant leap forward for team-maintained software.

The name: any keys not part of the CPAN Metadata Specification must be prefixed with “x_” – eventually, once it is used by more people and accepted into the specification, this name will become, simply, “authority.”

Other comaintainers: if Charlie joined the project prior to Bob‘s upload of Acme::Library::Other, then Alice still needs to grant co-maintainer permissions to Charlie. Unfortunately, the PAUSE Indexer cannot automatically grant permissions to him, since it has no notion of a “distribution,” only module namespaces.

Malicious uploaders: in the worst case, if Eve joins the project and maliciously (or unintentionally!) changes the x_authority, she will automatically get first-come permissions on the namespace of any modules she adds. However, this is the same behaviour that we had in the absence of x_authority.

Conclusions

Ultimately, the benefits of this feature (making group maintenance easier) drastically outweigh the cost (only a few small changes need to be made to the PAUSE Indexer). They are unlikely to cause any problems in practice, and the worst-case behaviour is the same as if we did not have x_authority at all.

It isn’t perfect, but it is a solution that requires minimal effort and minimal changes to PAUSE. Eventually, the goal is to create a more sophisticated system that will handle the issues outlined above, as well as more complex ones, such as renaming distributions or moving modules between distributions.

Thanks to Florian Ragwitz for spending some time discussing x_authority at length with me. He and Leon Timmermans proofread this article prior to publication.

Smarter Electric Distribution Systems: Case Studies (Part 2 of 2)

This is the second part of a two-part series (the first part provides an introduction) discussing the role of smart grids in electric power distribution systems. We will explore some past and current installations of smart grids, discussing their motivating factors, planning, implementation and results. Essentially, this article is a discussion where we learn both from our successes and our failures in the power industry, to inform our future decisions.

Netherlands

Smart meters are the some of the earliest intelligent devices installed in distribution networks and critical to enabling the smart grid of the future.  One of the biggest issues that every smart grid initiative encounters when attempting to incorporate the technology into their system is the public perception that smart meters violate the right to privacy.  Consequently, if the utility does not handle the situation tactfully, the reduction in the rate of consumer participation can diminish the practical gain from smart grid installations.

As mentioned previously, smart meters are capable of communicating wirelessly with the utility, receiving consumer usage data with the potential to control OpenHAN-compliant appliances remotely.  In the face of intelligent adversaries with increasingly powerful computing systems, it is important to provide a significant degree of security and future proofing.

In 2005, the Netherlands electricity distribution company Oxxio began widespread introduction of a smart meter for both gas and electricity.  When the European parliament issued a directive to member states to begin installation of smart metering equipment, the public was neither educated nor reassured about the new technology.  Economy minister Maria van der Hoeven decided to push for compulsory installation of smart meters and punishing refusal to install them with a fine of up to €17,000 or six months in prison.  Amidst privacy concerns, consumer protection organizations fought rigorously against the law and won; smart meters can now only be installed on a voluntary basis as requested by consumers [1].

We must learn from this stark lesson and avoid a similar outcome in future installations by ensuring adequate education for the public in order to assuage their fears and uncertainty, ultimately to ensure vital consumer participation.

Ontario

While the amount and timing of data provided by smart meters from the field does not pose serious privacy risks from internal misuse, there many security concerns surrounding external adversaries.  In particular, there is the potential for malicious users to modify their usage data in order to influence consumer billing, either by reducing their own consumption or as a financial attack against someone else.  Since the utilities would be making design decisions based on the recorded trends, outside manipulation of the data could cause catastrophic effects to equipment if not upgraded when needed due to underrepresentation of actual power consumption.

In Ontario, the current smart grid deployment initiative involves the government, Hydro One’s distribution business as well as other local utilities.  It demonstrates the need for very close cooperation between the utilities and their regulatory bodies, especially since much of their current success can be attributed to their work communicating with users.  Learning from errors in past smart grid implementations, the Ontario government established several websites acting as a central point of origin describing smart meters, their function and their overall objectives.

For support for the technical aspects of the deployment, Hydro One has partnered with Trilliant Technologies, which is a company that “provides intelligent network solutions and software to utilities for advanced metering, and Smart Grid management” [2].  Trilliant’s expertise and extensive smart metering technology portfolio reduces Hydro One’s risk and guarantees a higher degree of flexibility than with other vendors.  The smart meters operate in the unlicensed 2.4GHz radio frequency commonly used for ZigBee, Wireless LAN (IEEE 802.11) and Bluetooth, with Trilliant providing both the metering and the related communication infrastructure.  Trilliant also designed the 1.3 million smart meters currently being deployed by Hydro One’s distribution arm.

Thus far, current efforts to ensure network security and likewise to assure and encourage consumer participation in Ontario have been a success, and there are many other similar efforts taking place in other countries at this time.  Because smart meters involve using an extremely complex device to do measurement for billing purposes, it must be completely free of defects, especially in light of Canadian requirements like the Weights & Measures Act.

Australia

As climate change raises the average global temperature, Australia’s climate is one of the hardest hit: becoming hotter and drier than ever before.  Australia continues to consume a considerable amount of electricity; in fact, 261.8 TWh of electricity was produced in Australia during 2006, and that figure is projected to reach 413 TWh by 2030 [3].

With electricity demand continuing to rise, the utility may soon need to consider construction of new generation, transmission and distribution infrastructure.  However, maintenance of an aging system is itself extremely costly, and simultaneously investing in new infrastructure is simply not feasible.  As a result, Australia decided to implement dynamic rating of equipment in both their transmission and distribution systems, allowing them to better utilize existing infrastructure.  For an example comparing static equipment ratings with those dynamically generated by Australia’s control system, see Dynamic Equipment Rating.

[1]	Wilmer Heck. (2009, April) Smart energy meter will not be compulsory. [Online].   http://www.nrc.nl/international/article2207260.ece/Smart_energy_meter_will_not_be_compulsory
[2]	Trilliant, Inc. (2010, March) Trilliant, Inc. – Communications for the Smart Grid. [Online].   http://www.trilliantinc.com/
[3]	Cagil Ozansoy, “Turning Down the Heat,” Australia’s Fast-Growing Electricity Sector Ramps Up Its Global Warming Initiatives, vol. 8, no. 1, pp. 29-36, January-February 2010.

–

I originally wrote this article for a report submitted to ECE4439: Conventional, Renewable and Nuclear Energy, taught by Professor Amirnaser Yazdani at the University of Western Ontario.